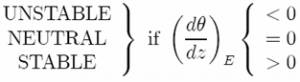Introduction | Tank – How to | Tank – Examples | Atmospheric_Examples | Theory | For_Teachers | Wiki
Stability
The main factors that drive convection are related to the buoyancy of a parcel of fluid within a fluid medium. For the purposes of exploring buoyancy, we will think of a column filled with a nearly incompressible fluid, such as water. Lets assume a horizontally uniform state with temperature T as a function of height z, T(z), and density as a function of height, ρ(z),
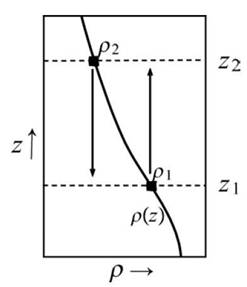
as illustrated in Fig. 1.
Fig. 1. The parcel at height z1 is at equilibrium since its density matches the environmental density. When moved to z2, the parcel will return towards, or accelerate away from, its initial position depending on whether it is heavier or lighter than the environment at height z2.
To start off, buoyancy is related to the density and the temperature of the fluid. If there is a change in temperature at one point of the fluid, the density will be:
where α is the thermal expansion constant for water for when T = Tref.
Let’s now consider a parcel of water in Fig. 1 at a height of z1. We suppose that it has the same temperature and density as the environment around it and will therefore be neutrally stable and at equilibrium.
Now, suppose we move the parcel, adiabatically (no heat is added to the system) such that temperature is conserved, to a height of z2. At that point, the parcel still has a temperature of T(z1) and a density of ρ(z1), but the surrounding environment has a temperature of T(z2) and a density of ρ(z2). Whether the parcel accelerates away or returns back toward its equilibrium position, will depend on the density of the parcel in relation to that of the environment at level z2. The density of the environment at level z2 is..
ρ(z2) = ρ(z1) + (∂ρ/∂z)Δz
Hence we can deduce from this exercise that the conditions for buoyancy in an incompressible, inviscid fluid are:

We see that an incompressible fluid is unstable if the density increases with height, the intuitive result.
We can also express these conditions in terms of temperature below since we have assumed that density depends only on temperature:
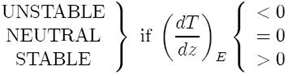
After convection has occurred, the fluid will be well mixed with constant temperature, the state of “neutrality”.
Potential Temperature
We have observed in our experiment that in thermal convection of an incompressible fluid such as water, temperature is mixed, and continually reset, to a constant temperature. But this not true of a compressible fluid such as air. In adiabatic motion of a dry air parcel, potential temperature, is conserved:
where θ is the potential temperature, κ is approximately 2/7, p is the current pressure, p0 is the reference pressure, and T is the temperature at the reference pressure.
The stability condition for dry convection of a compressible fluid expressed in terms of potential temperature can then be written:
which is directly analogous to that of an incompressible fluid. Therefore in the atmosphere convection will occur if dθ/dz is negative, and, after convection, just as in our tank experiment, the resulting convective layer will be well mixed with constant potential temperature. Convection returns the fluid to one of neutral stability in which θ = constant.