Introduction | Tank – How to | Tank – Examples | Theory | Wiki
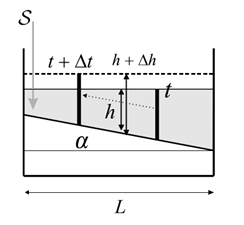
Consider the schematic diagram below. If fluid is introduced to the tank of side L at rate S, then the depth of the fluid in the tank, h increases at a rate given by
dh/dt = S/L²
In the presence of rotation, columns of fluid in steady, slow, frictionless motion must, by the Taylor-Proudman theorem, remain of constant length. Hence, if the free surface rises, an interior column, marked by the thick vertical line in the figure, must move toward the shallow end of the tank conserving its length. In a time Δt the free surface has risen by Δh and so the vertical velocity is:
w = Δh/Δt = S/L²
from above.
Given that the displacement of the column must match the geometry of the wedge defined by the upper surface and the sloping bottom, we see that the vertical and horizontal velocity must be in the ratio
w/v = dz/dy = α
where α is the slope of the bottom and we have used the definitions w = dz/dt; v = dy/dt where y is our coordinate increasing polewards, to the shallow end of the tank. Thus v is givenby:
v = w/α = (1/α)(S/L²).
The column moves polewards, towards the shallow end of the tank.