Balanced Motion: Theory-Note

Introduction | Tank – How to | Tank – Examples | Atmosphere – Examples | Theory | For Teachers | Wiki

Transforming from Pixel coordinates to Cartesian and Polar coordinates
The particle tracker measures coordinates in pixel rather than physical units. Before we begin to analyze the data it is best to convert it in to a more conventional coordinate system. The procedure is illustrated in Fig.3.

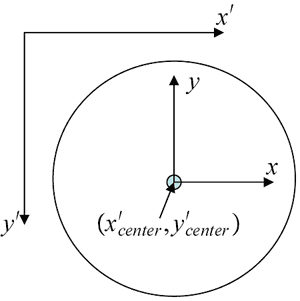
Fig.3 The particle tracker outputs positions in (x’,y’) coordinates, increasing to the right and downwards respectively. Let the origin of another (x,y) coordinate system be at (x’_center,y’_center). This system can be used as the starting point from which to express the position of the particle in (r,θ) coordinates shown in Fig.4 relative to the axis of rotation

The particle tracker outputs data in an (x’,y’) coordinates as shown in the figure. To convert to an (x,y) coordinate system that has its origin (0,0) at (x’_centery’_center) we use the transformation

and

To express the position and speed of the particle in polar coordinates we use the transformations (see Fig.4):

Having determined r and θ we can now compute (vr,v?) thus:

where the Δr (etc) are the small changes in r over successive time intervals computed from the particle tracker data. If Δt is assumed sufficiently small then the discrete evaluation of the gradient is a good approximation to the true gradient.

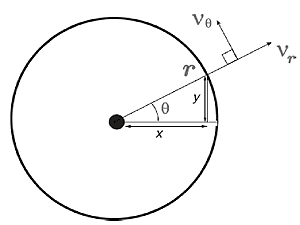
Fig.4 The velocity of a fluid parcel viewed in the rotating frame of reference: v_rot = (v_θ , v_r) in polar coordinates

Scaling between pixel units and physical units
To deduce speeds in physical units it is necessary to convert between pixel units and physical units. This can readily be done by determining the scale factor by viewing a ruler through the particle tracker and noting its physical length. Note that, due to camera distortions, this scale factor can change, particularly in the radial inflow experiment as the water drains away and the particles circulating on the surface move further away from the camera.