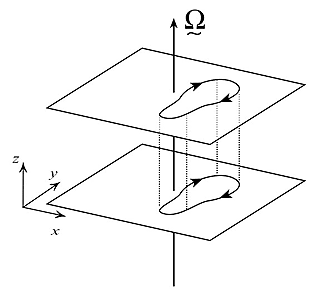
The key to understanding the glorious dye patterns seen in our dye-stirring experiment is the rigidity imparted to the fluid by rotation. A rotating fluid, brought in to gentle motion by stirring, is constrained to move in two-dimensions. Rich dye patterns emerge in planes horizontal to the rotation vector, but with strong vertical coherence between the levels: flow at one horizontal level moves in lockstep with the flow at another level, as illustrated in the diagram below.
In contrast a stirred non-rotating fluid mixes in three dimensions and has an entirely different character with no vertical coherence.
This rigidity, imparted to a fluid by virtue of it being in a rotating frame, is encapsulated in the Taylor-Proudman theorem which says that, under stated conditions – slow, steady, frictionless flow of a fluid of constant density – the velocity, both horizontal and vertical components, cannot vary in the direction of the rotation vector.
In the above image, slow, steady, frictionless flow of a rotating fluid of constant density, is two-dimensional: flow in a surface perpendicular to the rotation vector, moves in lockstep with flow at another level.
The Taylor-Proudman theorem is a consequence of the flow being geostrophic (small Rossby number), the fluid being homogeneous (constant density) and inviscid (no friction).
Relevant theory can be found in the discussion of balanced flow in Chapter 7 here.
Geostrophic balance (Section 7.1)
Taylor-Proudman theorem (Section 7.2)
See also the introductory comments here (Section 0.2.2).