Introduction | Tank – How to | Tank – Examples | Atmosphere – Examples | Theory | For Teachers | Wiki
We develop here some background theory for curved flow, appropriate to the radial inflow tank experiment and to the atmospheric example of hurricane flow.
Tank experiment
Force balances in the momentum equations
In the limit in which the tank is rotated rapidly, parcels of fluid circulate around many times before falling out through the drain hole (see, examples section); the pressure gradient force directed radially inwards (set up by the free surface tilt) is in large part balanced by a centrifugal force directed radially outwards.
If Vθ is the azimuthal velocity in the absolute frame of reference and vθ is the azimuthal speed relative to the tank (measured using the camera co-rotating with the apparatus) then:
where Ω is the rate of rotation of the tank in radians per second. Note that Ωr is the azimuthal speed of a particle stationary relative to the tank at radius r from the axis of rotation.
We now consider the balance of forces in the vertical and radial directions, expressed first in terms of the absolute velocity Vθ and then in terms of the relative velocity vθ.
Vertical force balance
We suppose that hydrostatic balance pertains in the vertical. Integrating in the vertical and noting that the pressure vanishes at the free surface (actually p = atmospheric pressure at the surface, which here can be taken as zero), and with ρ and g assumed constant, we find that:
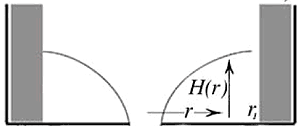
where H(r) is the height of the free surface (where p = 0) and we suppose that
z = 0 (increasing upwards) on the base of the tank.
Fig.1 The outer radius of the bucket is r1 and the height of the free surface H.
Radial force balance in the non-rotating frame
If the pitch of the spiral traced out by fluid particles is tight (i.e. in the limit that vr/vθ << 1 (where vr is the radial speed and vθ is the azimuthal speed) appropriate when Ω is sufficiently large) then the centrifugal force directed radially outwards acting on a particle of fluid is balanced by the pressure gradient force directed inwards associated with the tilt of the free surface. This radial force balance can be written in the non-rotating frame thus:
Using Eq.2, the radial pressure gradient can be directly related to the gradient of free surface height enabling the force balance to be written
Radial force balance in the rotating frame
Using Eq.1, we can express the centrifugal acceleration in Eq.4 in terms of velocities in the rotating frame thus:
Hence Eq.4 becomes
The above can be simplified by measuring the height of the free surface relative to that of a reference parabolic surface Ω2r2/(2g) as follows
Then, since ∂η/∂r = ∂H/∂r – Ω2r/g, Eq.5 can be written in terms of η thus:
Eq.4 (non-rotating) and Eq.6 (rotating) are completely equivalent statements of the balance of forces. The distinction between them is that the former is expressed in terms of Vθ, the latter in terms of vθ. Note that Eq.6 has the same form as Eq.4 except:
(i) η (measured relative to the reference parabola) appears rather than H (measured relative to a flat surface) and
(ii) an extra term, -2Ω vθ, appears on the rhs of Eq.6 — this is called the `Coriolis acceleration’. It has appeared because we have chosen to express our force balance in terms of relative, rather than absolute velocities.
Atmosphere – Example
Radial force balances
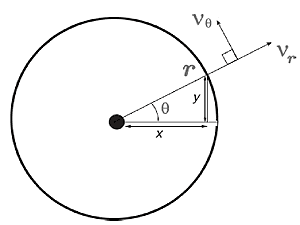
Consider parcels of air trapped in closed, axi-symmetric motion, moving with constant tangential velocity vθ along a path of curvature r:
Fig.2 The velocity of a fluid parcel viewed in the rotating frame of reference: vrot = (vθ , vr) in polar coordinates
The radial balance of forces away from frictional boundary layers and in the steady state is:
where g is the gravitational acceleration, f=2Ωsinφ is the Coriolis parameter and h is the height of a constant pressure surface.
Eq.7 is known as the `gradient wind’ relation. Note: Eq.7 has a similar form to Eq.6 in the tank experiment.
The Rossby number, Ro=vθ/fr measures the ratio of vθ²/r to fvθ. There are two limit cases:
If Ro<<1, then we have `geostrophic balance’:
If Ro>>1 then the `cyclostrophic’ relationship can be used:
The definition of the geostrophic wind from Eq.8:
can be used to rewrite the radial momentum equation, Eq.7, in the form
Dividing by fvθ , the ratio of the geostrophic wind to the actual wind can be written: