Introduction | Tank – How to | Tank – Examples | Theory | Wiki
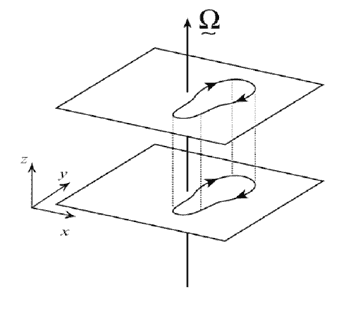
A remarkable property of the geostrophic motion of an inviscid homogeneous (ρ uniform) fluid is that it is two dimensional and does not vary in the direction of the rotation vector, Ω, as sketched in Fig.1. This property is summed up concisely in the Taylor-Proudman theorem. We derive it here.
If the flow is sufficiently slow and steady (i.e. Ro << 1) and frictional forces are negligible, then the momentum equation in a rotating frame of reference can be written:
where u is the flow vector, p is the pressure and φ is the gravitational potential (modified by centrifugal accelerations). The horizontal component of Eq.(1) yields geostrophic balance: the vertical component yields hydrostatic balance.
Taking the curl (∇x) of Eq.(1), we find that if the fluid is barotropic (i.e. one in which ρ = ρ(p)) then (noting that ∇·u = 0 and ∇x∇(scalar) = 0)
or (since Ω.∇ is the gradient operator in the direction of Ω i.e. z – see Fig.1)
Eqs 2 and 3 are equivalent statements of the Taylor-Proudman theorem (or T-P for short). T-P says that under the stated conditions — slow, steady, frictionless flow of a barotropic fluid — the velocity u, both horizontal and vertical components, cannot vary in the direction of the rotation vector Ω. In other words the flow is two–dimensional, as sketched in Fig.1. Thus, vertical columns of fluid remain vertical — they cannot be tilted over or stretched: we say that the fluid is made `stiff’ in the direction of Ω. The columns are called `Taylor Columns’ after G.I. Taylor who first demonstrated them experimentally.
Fig.1 The Taylor-Proudman theorem states that slow, steady, frictionless flow of a barotropic, incompressible fluid is 2-dimensional and does not vary in the direction of the rotation vector Ω.
The result Eq.(2) was first demonstrated by Joseph Proudman in 1915 but is now called the Taylor-Proudman theorem. Taylor’s name got attached because he demonstrated the theorem experimentally. In a paper published in 1921, he reported slowly dragging a cylinder through a rotating flow. The solid object all but immobilized an entire column of fluid parallel to the rotation axis.
Rigidity, imparted to the fluid by rotation, is at the heart of the glorious dye patterns seen in our dye-stirring experiment. On the right of Fig.2, the rotating fluid, brought in to gentle motion by stirring, is constrained to move in two-dimensions. Rich dye patterns emerge in planes perpendicular to Ω but with strong vertical coherence between the levels: flow at one horizontal level moves in lockstep with the flow at another level. In contrast, a stirred non-rotating fluid mixes in three dimensions and has an entirely different character with no vertical coherence; see the left frame of Fig.2.
Fig.2 Dye distributions from the dye stirring experiment: on the left we see a pattern from dyes (colored red and green) stirred into a non-rotating fluid in which the turbulence is three-dimensional; on the right we see dye patterns obtained in a rotating fluid in which the turbulence occurs in planes perpendicular to the rotation axis and is thus two-dimensional, as described in the Taylor-Proudman theorem.