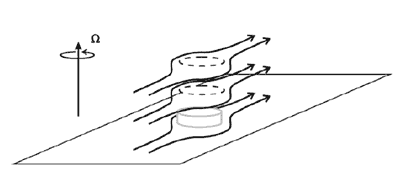
Suppose a homogeneous rotating fluid moves in a layer of variable depth, as sketched in Fig.1. This can easily be arranged in the laboratory by placing an obstacle such a hockey puck in the bottom of a tank of water rotating on a turntable and observing the flow of water past the obstacle.
The T-P theorem which pertains to a homogeneous (i.e. ρ uniform), rapidly rotating (i.e. Ro<<1), inviscid (frictionless) fluid (see theory section) states that
where Ω is the rotation vector and u if the fluid velocity. Thus fluid columns cannot be stretched in the direction of the rotation vector Ω and so act as if they were rigid moving along contours of constant fluid depth. Horizontal flow is thus deflected as if the obstacle extended through the whole depth of the fluid.
At levels below the top of the obstacle, the flow must of course go around it. But the Taylor-Proudman theorem says that the flow must be the same at all levels in the fluid: so, at all heights, the flow must be deflected as if the bump on the boundary extended all the way through the fluid! We can demonstrate this behavior in the laboratory, as described here.
Fig.1 The T-P theorem demands that vertical columns of fluid move along contours of constant fluid depth. Thus fluid columns act as if they were rigid and move along contours of constant fluid depth. Horizontal flow is thus deflected as if the obstacle extended through the whole depth of the fluid.