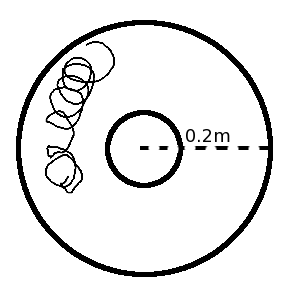Introduction | Tank – How to | Tank – Examples | Ocean – Examples | Theory
Ice cube experiment using an inclined plane
At a rotation rate of 15 rpm, the westward drift of the ice cube resulting from the Rossby waves induced by it can be clearly seen. However, due to the slow phase velocity of the Rossby waves, the drift is rather slow (see estimates of speed below). It is most clearly visible in the trajectories of tracked particles and in the accelerated movies below.
Fig.1. Accelerated movie (5x normal speed) of path followed by a square 1″ x 1″ x 1/2″ ice cube (click on the image to play the movie). Real time footage of the same ice cube can be seen in this movie.
We can now attempt to interpret the observed drift speed of the ice cube in terms of the phase speed of a Rossby wave. The ice cube takes approximately 180 seconds to travel 10cm across the tank, giving a phase speed of around 0.5mm/s. This is of the same order as that implied by the phase speed of the Rossby waves:
From the theory page, we can estimate the phase speed of the Rossby waves using the equation
cp = (gradient of tank depth)/H x Ω x λ2/4π2 (1)
Converting the rotation speed of 15rpm into rad/s, we get Ω = π/2 rad/s. The gradient of tank depth was 0.5, and the local depth 0.05m, which gives cp = 5λ2/4π. Estimating the wavelength as 0.05m from the wave observed in the above image, the phase speed comes out as cp = 1.0mm/s. The ice cube is close to attaining this speed in the later stages of motion.
The theory also suggests a cycloidal path is taken by the ice cube and the flow associated with it – this is clear if we track the paper dots near to the ice cube.
As predicted by theory, the larger, 2″ diameter cylindrical ice cubes move to the left more rapidly because the implied K is smaller (i.e., the lateral scale of the vortex is larger). The greater lateral displacement of water caused by the larger ice cube means that the generated vortices are more obvious. The ice cube shown below moves roughly 30cm in 180 seconds, which implies a phase speed of close to 1.5mm/s. An estimate of the wavelength of the Rossby wave from the distance between the two generated vortices (marked below) gives an answer of roughly 0.1m. Inserting this into the theoretical expression gives 4.0mm/s. Although this is somewhat faster than observed, higher than average speeds of this order do seem to be obtained during parts of the motion.
Fig.3. Accelerated movie (5x normal speed) of the path followed by a cylindrical 2″ diameter ice cube (click on the image to play the movie). Note the slightly cycloidal trajectory.
With the larger ice cubes, the westwards motion and vortex generation are particularly clear, although the greater vorticity of these generated vortices means that paper dots will often be dragged away from the ice cube, making it harder to investigate the path in an unambigious way.
Fig.4. Real time movie of path followed by a cylindrical 2″ diameter ice cube (click on the image to play the movie). Note the dye highlighting the vortices below the path of the ice cube. The generated vortices also propogate westwards due to the effects of Rossby waves.
Ice cube experiment using a cone
As in the experiment using an inclined plane, it is easiest to see the motion of the ice cube in an accelerated movie, although the motion is certainly quite noticeable even in real time.
Fig.5. Accelerated movie (5x normal speed) of path followed by a cylindrical 2″ diameter ice cube (click on the image to play the movie). Real time footage of the same ice cube can be seen in this movie.
Tracking particles placed on the ice cube from the above movie gives a trajectory similar to the epitrochoidal path predicted by theory:
Fig.7. Another accelerated movie (5x normal speed) of a path followed by a cylindrical 2″ diameter ice cube (click on the image to play the movie).
Again, we can use the footage to investigate whether the predictions from the theory are accurate. Using Eq.1 as in the case of using a plane, and substituting in Ω = π/3 rad/s (since the rotation speed is approximately 10rpm), a gradient of 1, local depth 0.05m, and assuming as in the experiment on a plane that the wavelength is roughly 0.1m, this gives cp ∼ 5mm/s.
In approximately 150s, the ice cube travels halfway round a circle of radius ≈ 0.1m. Hence the ice cube travels a distance ≈π/10, so this gives an average velocity of 2.0mm/s, which is certainly of the same order as the theoretical predictions.