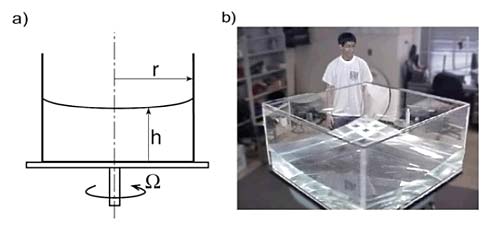
The depth of the rotating fluid in solid body rotation h is given by:
where r is the distance from the axis or rotation, Ω is the rate of rotation, g is the acceleration due to gravity and h(0) is the depth of the fluid at the origin (see diagram below). Thus the free surface takes on a parabolic shape: it tilts so that it is always perpendicular to the vector g* (gravity modified by centrifugal forces) given by
where Ω is the angular velocity vector, r is the position vector and z is a unit vector in the vertical. If we hung a plumb line in the frame of the rotating table it would point in the direction of g* i.e. slightly outwards rather than directly down.
Let us estimate the tilt of the free surface of the fluid by inserting numbers into Eq.(2) typical of our tank. If the rotation rate is 10 rpm (so Ω ~ 1 s-1) and the radius of the tank is 0.30 m , then with g = 9.81 m s-2, we find Ω2r2/(2g) ~ 5mm , a noticeable effect but a small fraction of the depth to which the tank is typically filled. If we increase the rotation rate to 30rpm, the deviation increases by a factor of 9, to 4 or 5 cm or so.
(a) Water placed in a rotating tank and insulated from external forces (both mechanical and thermodynamic) eventually comes into solid body rotation in which the fluid does not move relative to the tank. In such a state the free surface of the water is not flat but takes on the shape of a parabola. (b) parabolic free surface of water in a tank of 1m square rotating at Ω = 20 rpm.