We have seen that the free surface of the water in our rotating tank becomes deformed, taking on the shape of a parabolic surface which is perpendicular to the vector sum of gravity and the outward centrifugal acceleration. In direct analogy, over geological time the surface of the Earth adjusts to make itself an equipotential surface which is always perpendicular to the vector sum of Ω × Ω × rand g. This vector sum is `measured’ gravity:
g* = -gz – Ω × Ω × r.
We can compute the shape of a rotating, self-gravitating body as follows.
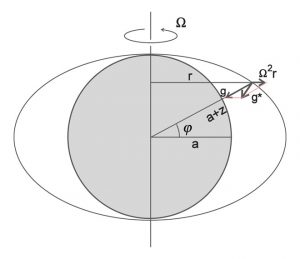
Fig.1 The centrifugal vector Ω×Ω×r has magnitude Ω²r, directed outward normal to the rotation axis. Gravity, g, points radially inwards to the center of the Earth. Over geological time the surface of the Earth adjusts to make itself an equipotential surface — close to a reference ellipsoid — which is always perpendicular the the vector sum of Ω × Ω × r and g. This vector sum is `measured’ gravity: g* = -gz – Ω × Ω × r.
Consider Fig. 1. The centrifugal vector Ω × Ω × r has magnitude Ω²r, directed outward normal to the rotation axis, where r = (a+z) cosφ ~ a cosφ, a is the mean Earth radius, z is the altitude above the spherical surface with radius a, and φ is latitude, and where the `shallow atmosphere’ approximation has allowed us to write a+z ~ a. Hence on the sphere the gravitational potential, phi
phi = gz – ((Ω²r²)/2
becomes:
phi = gz – ((Ω²a²cos²φ)/2)
defining the modified gravitational potential on the Earth. At the axis of rotation the height of a geopotential surface is geometric height, z, (because φ=(π/2)). Elsewhere geopotential surfaces are defined by:
z* = z + ((Ω²a²cos²φ)/(2g)). (1)
We can see that Eq.(1) is exactly analogous to that of the free surface of a fluid in solid body rotation in our rotating table — see Eq.(1) here – when we realize that r = a cosφ is the distance normal to the axis of rotation. A plumb line is always perpendicular to z* surfaces, and modified gravity is given by g* = – grad(z*).
Since (with Ω=7.27×10-5 s-1 and a=6.37×106m ) (Ω²a²)/2g ≈ 11km , geopotential surfaces depart only very slightly from a sphere, being 11km higher at the equator than at the pole. Indeed, the figure of the Earth’s surface — the geoid — adopts something like this shape, actually bulging more than this at the equator (by 21km , relative to the poles)
[Note: The discrepancy between the actual shape of the Earth and the prediction Eq.(2) is due to the mass distribution of the equatorial bulge which is not taken in the calculation presented here.]
Jupiter, because of its rapid rotation (period of rotation 9hours) and large size (it is approximately 10 times earth’s radius), is an oblate spheroid possessing a slight (6%) but noticeable bulge around the equator. Its equatorial radius is 71, 492 km and its polar radius is 66,852 km. Equation (1) predicts a bulge of 3900 km, given: Ω=2×10-4 s-1, a=6.6852 ×106m and g=23.13 ms-2.
This processed color image of Jupiter was produced in 1990 by the U.S. Geological Survey from a Voyager image captured in 1979. The colors have been enhanced to bring out detail.